A*算法实现流程图折线的思路
背景
在开发流程图时,节点之间的连线一般有三种类型:直线、曲线和折线
其中直线与曲线的实现比较简单,只要知道起点与终点就能计算出来,也不用考虑与流程图节点重叠的问题,直接穿过节点即可。
但是折线就不一样了,需要考虑节点避让,在合适的地方“拐弯”

那么,怎么确定这些拐点的位置?如何让折线避开节点,不与节点重叠?
可行的方法
拐点的位置,肯定是与节点的位置有关,而且跟连线的起点、终点坐标有关。
枚举法
知道了节点的相对位置与起点终点的坐标,就可以枚举出拐点了。也就是用 If Else 堆叠出来的枚举法,把所有可能的相对位置与起点终点都枚举出来,再去判断拐点的位置。
关于枚举法,如果条件不多的话是最简单的,但是两个节点的相对位置,加上起点终点的位置,这两个条件组合起来,有几十种情况,要全部写出来也是一件比较头疼的事。
网上也有总结出规律的简化版:流程图——正交连线的算法的一种简单实现
不过网上的枚举版本貌似都没有完全避开节点,还是会有重叠的情况。
寻路算法
相比枚举,用寻路算法就不那么头疼,节点相对位置与起点终点坐标对代码逻辑的影响会小一些,而且能很好地满足节点避让的条件,但需要先确定哪些坐标是连线可以到达的。
其他
应该有更好的解决方案,欢迎提出一起研究。
A* 算法
关于 A* 算法的解释,看这篇文章大概就能掌握: https://blog.csdn.net/hitwhylz/article/details/23089415
简单来说,目的就是找到从 A 点到 B 点的一条路径。
从 A 点出发,找出 A 点附近可到达的所有点,计算其 f 值,其中 f = g + h
g: 从起点到当前点的开销
h: 从当前点到终点预估的开销
找出 f 最小的点作为下一个目的,重复上述步骤
直到找到 B 点,或者无法到达 B 点为止。
地图构建
要应用寻路算法,首先要把地图画出来,也就是确定地图上有哪些点。
以像素作为路径点
如果把每个像素作为路径点,通过这个像素是否在节点内部来判断这个坐标是否可以走,地图的构建似乎十分简单。
实际上,用这样细粒度的地图来画线不是不行,如果起点与终点的距离比较近,寻路后遍历到的点就几十个。
但是随着用户拖动节点,这样构建的地图缺陷就很明显了:
- 节点每移动一次,路径都需要重新计算,一次几十个点看起来不是很多,但计算的频次变高之后,单位时间内需要遍历的点就越多
- 随着起点与终点距离的变化,需要遍历的点数量也不同,如果距离拉长,需要遍历的点数量就会暴增,达到几百个甚至几千个
最终导致的结果就是,程序卡顿,甚至卡死
尽量减少需要遍历的路径点
那么,是不是寻路算法就不能用在这里了?答案当然是否定的,通过观察流程图折线可以知道,一般拐点的个数也就两三个,而通过像素构建的地图,虽然精度高,但最后画出来的折线,拐点也还是两三个,整条路径上大部分都是直线。所以,大多数点都是不需要去遍历的,是我们构建地图的方法有问题。
因此需要尽量简化地图,减少遍历点的个数。
我们以最简单的起点终点位置为例:
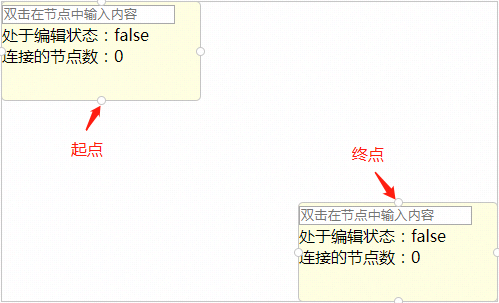
这时的折线连线显然是这样的:
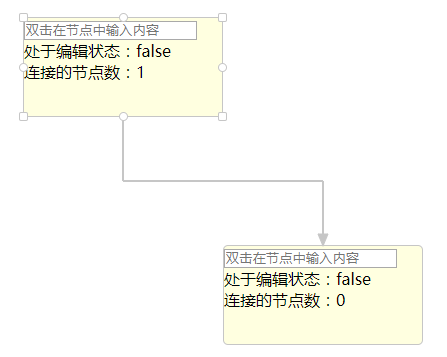
实际上,操作过几个流程图的实现后,可以发现,折线的拐点,为了避让节点,走向总是会环绕着节点:
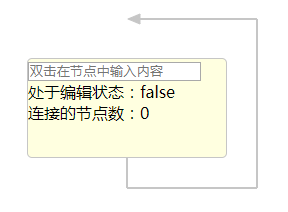
经过观察可以知道,折线的拐点总是出现在固定的几个位置:
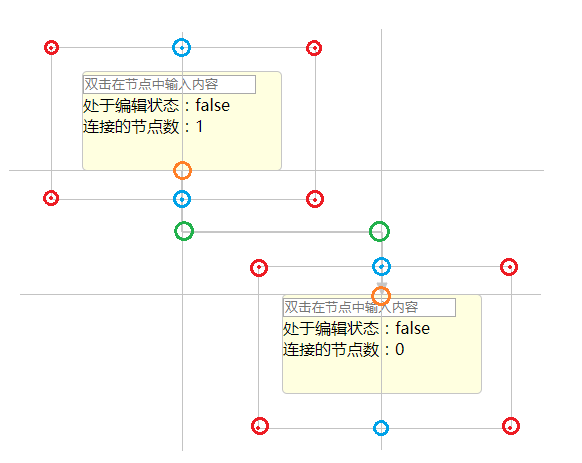
- 两个节点的四个边向外扩展一定边距组成的矩形的四个角(红色8个点)
- 起点与终点垂直于节点边做延长线,与扩展矩形的交点(蓝色4个点)
- 起点与终点分别做十字延长线组成一个矩形,矩形中垂直于节点边的两条边的中点(绿色2个点)
这样,拐点可能出现的坐标,一共 14 个点,再加上起点与终点 2 个点,最终构成了一个 16 个点的简化地图
以上考虑的是一个典型的流程图情况,除此之外,还有一些情况:
- 只有一个节点的情况
- 没有节点的情况
- 需要避让除了起点、终点所在节点之外的其他节点的情况(暂时不考虑)
以上几种情况对应的地图坐标点的数量都不相同,前两种情况数量较为固定,公式:
16 - 没有节点的数量(1 或者 2) x (扩展矩形的 4 个点 + 延长线与扩展矩形的 2 个交点(蓝色)) + 没有节点的数量(1 或者 2) x (起点与终点十字延长线组成矩形的中点 1 个 + 起点与终点十字延长线组成矩形的 1 个角)
比如,连线只有一个节点时,地图点数 = 16 - 1 x (4 + 2) + 1 x (1 + 1) = 12
只有连线,没有节点时,地图点数 = 16 - 2 x (4 + 2) + 2 x (1 + 1) = 8
除了不考虑的第三种情况,其他情况地图上的点数量都不超过 16 ,即寻路时遍历的点数不会超过 16 ,相比像素作为地图路径点,极大减少了遍历的数量。
附:当两个节点重叠,导致在避让节点的条件下没有路径时,则忽略两个节点,不进行避让,即第二种情况。
确定可到达的点
确定了地图上有哪些点后,接下来该找到一个办法,用来确定哪些坐标可以走,哪些坐标不能走。
与平常的 A* 不同的是,平时地图上的每个点已经确定是可走的或者是障碍物了,对于一个点 P 来说,无论算法遍历到哪个点,点 P 的属性都不会改变,是可走的,就一直是可走的,是障碍物就一直是障碍物。
而在流程图折线里,一个点是否可走,取决于当前遍历的点,点 P 有可能在遍历上一个点时是可走的,遍历下一个点时,又是不可走的。
假设现在用 A* 遍历到了下图蓝色的点:
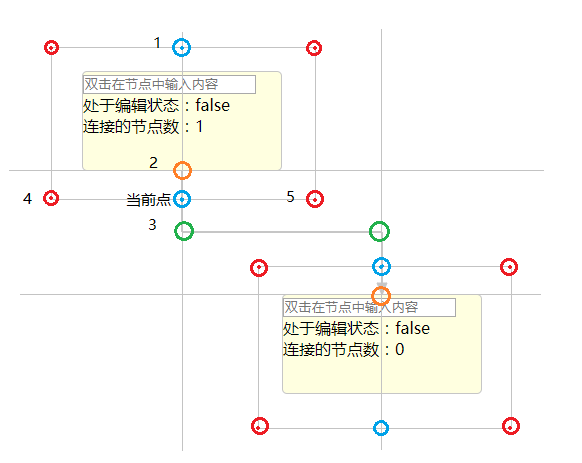
由于折线只有水平或者垂直两个方向的走向,下一个点只能在经过其十字延长线的点上去查找,在图上已标明共有 5 个点。
但是这 5 个点不能直接添加到 Open List 中,因为目前它们只是 “可能是可走的点” 。
如何确定是否真的可以走?只要把当前点,分别与 5 个点连起来,生成 5 条线,其中,线与节点重叠的点,即是不可走的点。
这个判断就是为了让折线能够避让节点。
其他优化
完成了地图构建与确定可到达点的方法后,剩下的就是按照 A* 算法的步骤去执行了。
不过执行后画出来的路径,虽然实现了弯折与节点避让,但有时候不是很美观,有时候路径不是我们想要的,比如:
- 折线没有经过中点
- 折线拐点太多
这时候就需要动到 A* 里面的核心公式了。
我们知道,决定下一个遍历的点时,是以 f = g + h 中 f 的大小决定的,即取 f 最小的点,那么,在 f 相同的情况下,取的点就不确定了,一般是取先进入 Open List 的点。
为此,对 f 相同的点,可以进行一些额外的判断:
- 当 f 相同时,取 abs(g-h) 较小的点,以达到优先走中点的目的
- 当 f 与 abs(g-h) 都相同时,引入另外一个变量 t ,表示拐点的数量,取 t 较小的点
经过优化,就大致可以达到我们想要的效果了。
项目
此流程图项目目前只能算个 Demo ,优化空间很大